La torre, el cubo y el tablero
La enigmática equivalencia de dos mitos: la Torre de Brahma y la recompensa que el inventor del ajedrez le pidió al rey de la India
EL PAÍS y Materia proponen a sus lectores, cada semana, un juego de lógica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta será ofrecida en la columna de la semana siguiente.
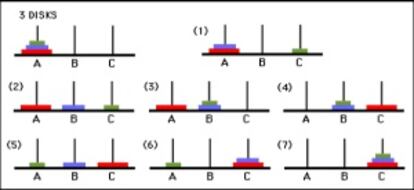
Para hallar la secuencia de movimientos necesarios para trasladar los discos de un eje a otro en la torre de Hanói de tres discos de la semana anterior, partamos del caso más sencillo posible: una torre trivial de un solo disco, en la que es evidente que basta un movimiento para trasladar ese disco a otro eje. Una torre de dos discos también es trivial: trasladamos el menor a uno de los dos ejes libres, el mayor al otro eje libre, y por último ponemos el menor sobre el mayor. Consideremos ahora nuestra torre de tres discos, que numeraremos de menor a mayor: 1, 2 y 3. Para el primer movimiento solo hay una opción: trasladar el disco 1 a uno de los dos ejes libres. Para el segundo movimiento solo hay una opción no repetitiva: pasar el disco 2 al eje libre. Los siguientes movimientos no son únicos, pero sí bastante obvios: 3º) 1 sobre 2, 4º) 3 al eje libre, 5º) 1 al eje libre, 6º) 2 sobre 3, 7º) 1 sobre 2. La secuencia es, pues, 1213121.
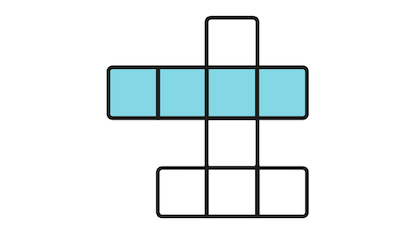
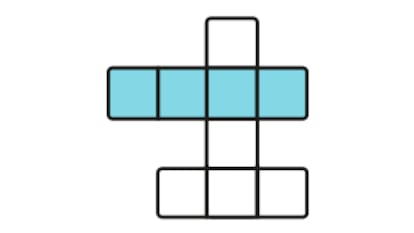
Como vimos, William Hamilton estudió en todos los sólidos platónicos, y no solo en el dodecaedro, los recorridos que llevan su nombre. En el caso de un cubo, si llamamos 1 a la dirección vertical, 2 a la horizontal y 3 a la anteroposterior, partiendo, por ejemplo, del vértice A del cubo de la figura y efectuando el sencillo recorrido hamiltoniano AEFBCGHD, que pasa por todos los vértices una sola vez, vemos que la secuencia direccional (y dimensional) del ciclo es 1213121, la misma que en una torre de Hanói de tres discos.
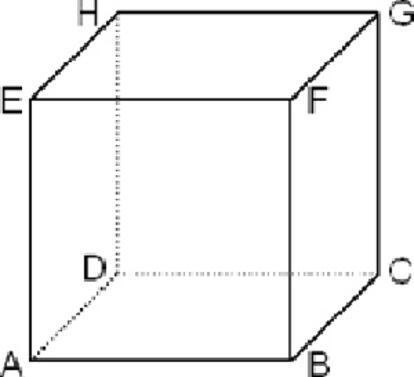
Y, como también vimos la semana pasada, a mediados del siglo pasado D. W. Crowe demostró que este sorprendente isomorfismo se mantiene para torres de cualquier altura y cubos de cualesquiera dimensiones: el orden en el que hay que mover n discos de una torre de Hanói para trasladarlos a otro eje, se corresponde exactamente con la secuencia direccional (y dimensional) de un recorrido hamiltoniano en un cubo de n dimensiones.
Por otra parte, y como es bien sabido, el mítico inventor del ajedrez le pidió al rey de la India un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta, y así sucesivamente hasta la casilla 64, doblando en cada una el número de granos de trigo de la anterior. Pues bien, este número astronómico (18.446.744.073.709.551.615) es igual al número de traslados necesarios para pasar de un eje a otro los 64 discos de oro de la torre de Brahma (y también, como acabamos de ver, al número de aristas que hay que recorrer en un hipercubo de 64 dimensiones para efectuar un ciclo hamiltoniano).
¿Cómo se explica la sorprendente equivalencia?
Carlo Frabetti
Escritor y matemático, miembro de la Academia de Ciencias de Nueva York, ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’