Matemáticas para apilar naranjas
El problema del empaquetamiento de esferas, que interesa a los matemáticos desde hace siglos, tiene aplicaciones en áreas como la corrección de códigos

Cualquier frutero lo tiene claro: la mejor forma de colocar naranjas, ocupando el menor espacio posible, —el denominado problema del empaquetamiento de esferas—, consiste en formar con ellas una pirámide, en la cual cada capa de naranjas se asienta sobre los huecos de la capa inferior. Pero realmente, de entre todas las disposiciones posibles de naranjas, ¿es esta la que mejor aprovecha el espacio? El problema, que es mucho más complejo de lo que pudiera parecer, fue resuelto hace nada más que 25 años y la comprobación de que la respuesta era correcta duró casi 20 años.
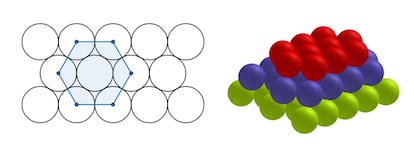
El problema fue propuesto en 1611 por el ilustre científico Johannes Kepler. Conjeturó que, en su versión en dos dimensiones —que consiste en determinar cuál es la manera óptima de colocar círculos en un plano— una disposición análoga en dos dimensiones a la de la pirámide —siguiendo un patrón hexagonal—, era la óptima. La demostración rigurosa de esta afirmación llegó en 1942, de manos del matemático húngaro László Fejes Tóth, quien concluyó una demostración incompleta de Axel Thue, propuesta en 1890.
El problema de las esferas tridimensionales resultó ser más difícil aún. Hubo que esperar hasta 1998 para que publicó el matemático estadounidense Thomas C. Hales demostrase que el empaquetamiento de esferas óptimo en tres dimensiones es el que sigue la disposición de pirámides. En su demostración usaba, además, algunos cálculos hechos con ordenadores y la prueba de que dichos cálculos eran correctos se demoró hasta 2014.
Los matemáticos han estudiado también empaquetamientos en dimensiones más altas que, además, tienen aplicaciones en áreas como la corrección de códigos. Si tratamos cada mensaje de (a lo sumo) 20 bits de longitud como un vértice de un cubo 20 dimensional, podemos aprovechar buenos empaquetamientos de esferas en dimensión 20 para corregir mensajes erróneos.
Concretamente, si recibimos un mensaje que no entra dentro de nuestra lista de mensajes admisibles —ya sea porque no tenga sentido o porque tengamos una lista preestablecida de mensajes que consideramos admisibles—, podría significar que ha habido un fallo en el canal de comunicación y, en tal caso, sería bueno poder corregirlo. Para intentar averiguar cuál era el mensaje inicial, podemos buscar el mensaje, de entre todos los admisibles, que es más parecido al que hemos recibido. Para ello, simplemente se comparan distancias en el espacio 20-dimensional de los mensajes.
Así, si disponemos de buenos empaquetamientos de esferas de dimensiones altas, podemos interpretarlas como mensajes admisibles que permiten corregir errores en la comunicación. El hecho de que ocupen una fracción pequeña del espacio se traduce en que los mensajes utilizan la menor cantidad posible de bits.
Sin embargo, el problema de los empaquetamientos óptimos en dimensiones altas —mayores que tres— sigue siendo un problema abierto: solo se han encontrado las configuraciones óptimas en dimensión ocho y en dimensión 24.

El resultado en dimensión ocho fue demostrado en 2016 por la matemática ucraniana Maryna Viazovska, que acababa de terminar el doctorado en aquel momento. Es un hito muy destacado de la matemática reciente ya que, además, sus métodos simplificaban enormemente los que usaba Hales para demostrar el caso tridimensional. Lo cual no quiere decir, ni mucho menos, que la demostración fuera fácil: el trabajo aúna herramientas y técnicas del análisis de Fourier, de la teoría de números y del campo de la optimización. Además, con su demostración no era necesaria la ayuda computacional.
Con esta publicación, Viazovska adquirió rápidamente fama mundialmente y, junto con otros colaboradores, resolvió el problema en dimensión 24 un año después, adaptando los métodos ya usados en dimensión ocho. Sin embargo, estos métodos no parecen funcionar —sin modificaciones importantes— para más dimensiones y nadie ha conseguido resultados definitivos en cualquier otra dimensión hasta la fecha. Para algunas de las demás dimensiones se ha demostrado que algunas de las conjeturas actuales son bastante cercanas al óptimo, pero no hay demostraciones completas.
¿Se resolverá el problema de los empaquetamientos de esferas en alguna otra dimensión pronto? Eso ya entra en el terreno de la especulación. Pero de lo que podemos estar seguros es de que, aparte del interés que pueda suscitar el resultado, es probable que lo más destacable de una demostración en este sentido sea una nueva conexión profunda entre distintos campos de las matemáticas —como pasó con la demostración de Viazovska—, algo que siempre es muy deseable para abrir nuevas líneas de investigación.
Pablo Hidalgo Palencia es investigador predoctoral en el ICMAT
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Más información

Cinco años sin Maryam Mirzakhani, exploradora de superficies