Nanotubos y neuronas
¿Podría haber una relación directa entre los microtúbulos neuronales y la consciencia?

Nuestras galletas circulares de la semana pasada, al crecer dentro del horno y comprimirse mutuamente, formarían (formaron: me sucedió realmente) una red hexagonal semejante a la de un panal de abeja. De hecho, las abejas no construyen hexágonos directamente, sino que van formando celdillas circulares —cilíndricas, quiero decir— que al crecer y apretarse unas contra otras dan lugar a la consabida configuración hexagonal.

Se sabe desde antiguo que un teselado hexagonal, o sea, una retícula en forma de panal de abeja, es la forma óptima de dividir una superficie en zonas de la misma área y con el mínimo perímetro total; pero hasta finales del siglo pasado solo fue una conjetura (no en vano denominada la “conjetura del panal de abeja”). La conjetura, ahora ya teorema, fue demostrada en 1999 por el matemático estadounidense Thomas Callister Hales.
El hexágono es uno de los tres polígonos regulares que pueden teselar el plano, junto con el cuadrado y el triángulo equilátero. Si formáramos una superficie plana pegando entre sí, por los bordes, teselas hexagonales regulares, ¿cuál sería el ahorro en pegamento con respecto a la misma superficie formada por cuadrados iguales, también pegados entre sí poniendo pegamento en todos sus bordes y en toda la longitud de los mismos? (Se considera una gran superficie que permite despreciar el hecho de que el perímetro de un área teselada con hexágonos es una línea quebrada).
Nanotubos de carbono
Un nanotubo es una estructura química cilíndrica cuyo diámetro es del orden de los nanómetros (recordemos que un nanómetro es la millonésima parte de un milímetro). Aunque los hay de otros materiales, los nanotubos por excelencia, como veíamos la semana pasada, son los de carbono, que vienen a ser como diminutas láminas de grafito de un solo átomo de grosor (o lo que es lo mismo, de grafeno) enrolladas y con los bordes unidos para formar un cilindro muy alargado, una especie de microcapilar de unas micras de longitud y un diámetro nanométrico. Por sus extraordinarias propiedades mecánicas, eléctricas y térmicas, las aplicaciones de los nanotubos son muchas y muy prometedoras, sobre todo en la miniaturización de componentes electrónicos, por lo que desempeñarán un papel fundamental en el futuro desarrollo de la informática.
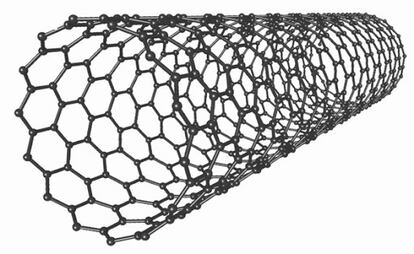
Los nanotubos pueden ser de pared simple (SWNT: Single-Walled NanoTube) o de pared múltiple (MWNT: Multi-Walled NanoTube). Los segundos pueden estar formados por varios tubos concéntricos, o bien por una lámina multicapa de grafito enrollada como un pergamino.
Tal vez las aplicaciones más espectaculares de los nanotubos se produzcan -se están produciendo ya- en el terreno de la neurofisiología. Se ha comprobado que pueden intervenir eficazmente en la formación de sinapsis, las estructuras a través de las cuales las células nerviosas se comunican entre sí, y también pueden propiciar el crecimiento de las neuronas. Esto significa que los nanotubos pueden facilitar la regeneración neuronal y crear un nexo artificial entre grupos de neuronas cuya conexión ha quedado interrumpida. Entre otras posibilidades, esta propiedad de los nanotubos de carbono -y también de otros materiales- abre un nuevo y esperanzador camino para el tratamiento de personas con daños en la médula espinal.
Y hablando de nanotubos y neuronas, cabe señalar que a finales del siglo pasado Roger Penrose (reciente premio Nobel de física por sus trabajos sobre los agujeros negros) y Stuart Hameroff sugirieron que la red de microtúbulos de las neuronas podría funcionar como un computador cuántico responsable de nuestra consciencia. La idea ha sido ampliamente debatida y en varias ocasiones refutada, pero abre una interesante vía de investigación.
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos ‘Maldita física’, ‘Malditas matemáticas’ o ‘El gran juego’. Fue guionista de ‘La bola de cristal’.
Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aquí a nuestra newsletter
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Sobre la firma































































