Matemáticas para explicar cómo se unen las células
La ecuación de agregación-difusión explica los diferentes patrones que se forman al mezclar dos poblaciones de células
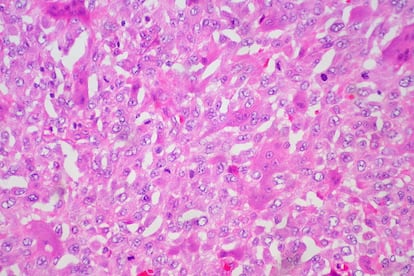
En la segunda mitad del siglo XX el biólogo Malcolm Steinberg, inspirado por el trabajo de Philip Townes y Johannes Holtfreter, llevó a cabo una serie de experimentos fundamentales para entender la formación de tejidos y órganos en organismos multicelulares como los humanos. En ellos, observó cómo dos poblaciones de células diferentes, inicialmente mezcladas, y sin ningún tipo de estructura, se organizaban para formar un patrón muy bien definido, con las dos poblaciones celulares separadas y con una de ellas envolviendo a la otra.
Además, Steinberg observó que podía obtener más patrones utilizando diferentes tipos de células como poblaciones iniciales. Para ciertos tipos de células, las dos poblaciones se mantenían mezcladas y sin ningún tipo de estructura, como al inicio del experimento. Con otros tipos de células, sin embargo, la separación entre las dos poblaciones al final del experimento era todavía más clara.
La aparición de estos patrones diferentes llevó a Steinberg a formular una explicación basada en ideas físicas simples, que ahora se conoce con el nombre de hipótesis de adhesión diferencial. Esta estipula que la responsable de estos patrones es la adhesión celular entre las diferentes poblaciones, es decir, la fuerza con la que las células se unen a otras células de su mismo o diferente tipo.
Básicamente, la hipótesis de Steinberg dice que las células se comportan como dos líquidos con tensiones superficiales diferentes, como, por ejemplo, agua y aceite. De esta manera, al igual que la alta tensión superficial del agua y del aceite provoca que ambos líquidos no se mezclen, dos poblaciones celulares con una gran adhesión celular hacia células de su mismo tipo tenderán a mantenerse separadas. Por el contrario, cuando la adhesión celular hacia células de otro tipo es fuerte, las dos poblaciones tenderán a mezclarse. Esta hipótesis permite entender cómo poblaciones de células se pueden organizar para formar estructuras complejas, y ha sido corroborada en múltiples experimentos.
Las células se comportan como dos líquidos con tensiones superficiales diferentes. Al igual que el agua y aceite, no se mezclan. De esta manera, dos poblaciones celulares se mantienen separadas
En la actualidad, la adhesión celular continúa siendo fundamental en experimentos que tratan de explicar cómo se forman tejidos y órganos durante el desarrollo embrionario. Pero ahora parte de estos experimentos se pueden simular mediante un ordenador, con un coste —de tiempo y dinero— mucho menor. Además, muchas veces, estos ofrecen una explicación más completa de la física que hay detrás del movimiento celular. Para ello, necesitamos modelos matemáticos que reproduzcan, mediante ecuaciones, los fenómenos observados.
En el caso de la adhesión celular, los modelos matemáticos se basan en dos ideas sencillas. Primero, se considera una fuerza atractiva que provoca que las células que están cerca traten de mantenerse unidas, imitando el proceso de adhesión celular. Según las diferentes adhesiones entre tipos de células se consideran fuerzas de atracción de distinta intensidad.
Por otra parte, se asume que el movimiento de cada célula o de grupos de células tiene un carácter más o menos aleatorio. Combinando ambas ideas se llega a un conocido modelo dado por la ecuación de agregación-difusión, una ecuación diferencial en derivadas parciales que describe la evolución temporal de una función, que representa la densidad de células en cada punto del espacio.
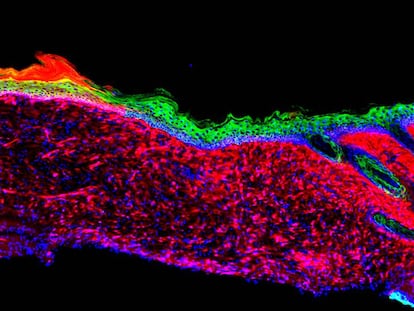
La ecuación de agregación-difusión se puede aplicar a sistemas con dos o más poblaciones de células. En este caso, se obtiene un sistema de ecuaciones en derivadas parciales para las diferentes densidades de células. En particular, variando la intensidad de las diferentes fuerzas de atracción es posible reproducir los patrones observados en los experimentos de Steinberg. En la imagen se muestra el resultado de resolver este tipo de ecuaciones para dos poblaciones, representadas en rojo y verde, junto con un esquema de los posibles patrones obtenidos.
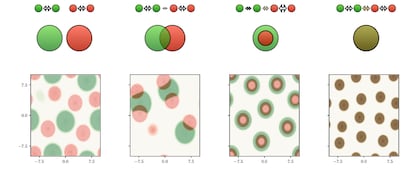
Con estas ecuaciones de agregación-difusión podemos describir el proceso de adhesión celular, así como su impacto en la organización y movimiento celular. Este modelo ha generado mucho interés en la última década, no solo por sus aplicaciones en biología y sus propiedades matemáticas, sino también por las nuevas técnicas de análisis matemático que ha motivado. La existencia y unicidad de soluciones del sistema de ecuaciones resultante, así como otras propiedades estructurales, son solo algunas de las preguntas que han surgido gracias a la investigación en este campo.
Carles Falcó es investigador predoctoral en el Instituto de Matemáticas de la Universidad de Oxford (Reino Unido) y becario de la Fundación “la Caixa”
Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).
Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.